机器学习必修之数学基础系列课程

本节课主要讲了奇异值分解（svd），以及其在PCA（主成分分析）中的应用。

1.奇异值分解：

奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解：

假设A是一个m*n的矩阵，那么得到的U是一个m*m的方阵，U里面的正交向量被称为左奇异向量。Σ是一个m*n的矩阵，Σ除了对角线其它元素都为0，对角线上的元素称为奇异值。是v的转置矩阵，是一个n*n的矩阵，它里面的正交向量被称为右奇异值向量。而且一般来讲，我们会将Σ上的值按从大到小的顺序排列。
 

2.PCA

在之前课程我们学习过特征值分解，其实PCA可以通过两种方式来实现，一种是基于特征值分解，一种是基于svd分解。两种的方法如下：

1）基于特征值分解：

对于矩阵A，有一组特征向量v，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下式：

其中，Q是矩阵A的特征向量组成的矩阵，则是一个对角阵，对角线上的元素就是特征值。

具体实现方法：
 

输入：数据集，需要降到k维。
1) 去平均值(即去中心化)，即每一位特征减去各自的平均值。、

2) 计算协方差矩阵,注：这里除或不除样本数量n或n-1,其实对求出的特征向量没有影响。

3) 用特征值分解方法求协方差矩阵的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为行向量组成特征向量矩阵P。

5) 将数据转换到k个特征向量构建的新空间中，即Y=PX。
 

2）基于奇异值分解：

奇异值分解是一个能适用于任意矩阵的一种分解的方法，对于任意矩阵A总是存在一个奇异值分解：

假设A是一个m*n的矩阵，那么得到的U是一个m*m的方阵，U里面的正交向量被称为左奇异向量。Σ是一个m*n的矩阵，Σ除了对角线其它元素都为0，对角线上的元素称为奇异值。是v的转置矩阵，是一个n*n的矩阵，它里面的正交向量被称为右奇异值向量。而且一般来讲，我们会将Σ上的值按从大到小的顺序排列。

具体实现方法：

输入：数据集，需要降到k维。

1) 去平均值，即每一位特征减去各自的平均值。

2) 计算协方差矩阵。

3) 通过SVD计算协方差矩阵的特征值与特征向量。

4) 对特征值从大到小排序，选择其中最大的k个。然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。

5) 将数据转换到k个特征向量构建的新空间中。
 

这节课主要讲了矩阵的QR分解和LU分解。具体内容如下：

这节课主要讲了矩阵的QR分解和LU分解。具体内容如下：

矩阵的LU分解是将一个矩阵分解为一个下三角矩阵与上三角矩阵的乘积。采用划十字的方法一步一步进行计算。

LU分解：

矩阵的LU分解是将一个矩阵分解为一个下三角矩阵与上三角矩阵的乘积。采用划十字的方法一步一步进行计算。

QR分解：

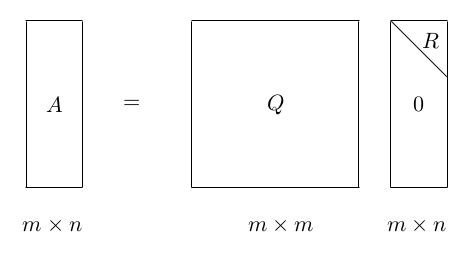
矩阵的正交分解又称为QR分解，是将矩阵分解为一个正交矩阵Q和一个上三角矩阵的乘积的形式。

任意实数方阵A，都能被分解为A=QR。这里的Q为正交单位阵，即QTQ=I。R是一个上三角矩阵。这种分解被称为QR分解。

QR分解也有若干种算法，常见的包括Gram–Schmidt、Householder和Givens算法。

课时3重点：线性变换，线性子空间，正交概念，矩阵的秩和逆，矩阵的条件数

基础概念：

秩：在线性代数中，一个矩阵A的列秩是A的线性独立的纵列的极大数目。类似地，行秩是A的线性无关的横行的极大数目。通俗一点说，如果把矩阵看成一个个行向量或者列向量，秩就是这些行向量或者列向量的秩，也就是极大无关组中所含向量的个数。

奇异矩阵：秩不为满秩的矩阵。

对于条件数的补充：

κ(A)=‖A‖‖A−1‖
κ(A)=‖A‖‖A−1‖
如果方阵 A 是奇异的，那么 A 的 condition number 就是正无穷大了。实际上，每一个可逆方阵都存在一个 condition number。

对condition number来个一句话总结：condition number 是一个矩阵（或者它所描述的线性系统）的稳定性或者敏感度的度量，如果一个矩阵的 condition number 在1附近，那么它就是well-conditioned的，如果远大于1，那么它就是 ill-conditioned 的，如果一个系统是 ill-conditioned 的，它的输出结果就不要太相信了。

应用
ŵ =(XTX)−1XTb
w^=(XTX)−1XTb
如果当我们的样本 X 的数目比每个样本的维度还要小的时候，矩阵XTXXTX将会不是满秩的，也就是XTXXTX会变得不可逆，所以ŵ w^就没办法直接计算出来了。

如果加上L2规则项，就变成了下面这种情况，就可以直接求逆了：

ŵ =(XTX+λI)−1XTb
 

-------

转自https://blog.csdn.net/lanchunhui/article/details/51372831