一、矩阵运算于图像处理:
0、像素取值范围是[0, 255];
1、矩阵加法,增幅较小,易使像素值大于等于255,因此在图像上即表现为白色噪声;
2、同理,矩阵相乘,增幅是成倍数的,因此易使像素取值集中到0或255,也就呈现出黑白相间的条纹状;
二、矩阵运算
1、AB≠BA
2、方阵的幂
¥
支付方式
请使用微信扫一扫 扫描二维码支付
请使用支付宝扫一扫 扫描二维码支付

一、矩阵运算于图像处理:
0、像素取值范围是[0, 255];
1、矩阵加法,增幅较小,易使像素值大于等于255,因此在图像上即表现为白色噪声;
2、同理,矩阵相乘,增幅是成倍数的,因此易使像素取值集中到0或255,也就呈现出黑白相间的条纹状;
二、矩阵运算
1、AB≠BA
2、方阵的幂
1、向量是带方向的标量,所以它的一个自然属性就是有序。
关于这一点,可以联系排列组合的概念理解:
(1)所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。
(2)组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
因此,关于向量相等的条件也就很清楚了,必须得一一相等。
2、向量内积(点乘,数量积)
(1)计算结果是一个数值。
(2)引入的素材是物理中的做功,功表示能量,其大小是数值。因此内积的结果也是数值。
(3)向量内积可用来判断两个向量是否正交(相互垂直)
3、向量范数
(1)之所以称为范数而不是长度,是因为生活中不同的应用场景所对应的“规则”不同, 称谓也不同,因此以“范数”来广泛定义。可与张量的概念相类比。
(2)0范数不是范数,因为它违反了向量范数定义的第2个条件——齐次性。
4、线性相关与线性无关
(1)向量组的秩
(2)极大无关组
5、由向量引出矩阵的概念
5.1 矩阵范数
6、作业
进入到凸优化,难度比以前加强了,主要是概念和定理比较多,比较抽象化,需要结合画图和例题来进行梳理。
1可行下降方向:
2.起作用约束(active constraint)
亦称紧约束或积极约束,是指在某可行点处使不等式约束成为等式的约束。对于可行点x',当gi(x')=0时点x'处于这个约束形成的可行域的边界上,起到了限制作用,故称这一约束为点x'处的起作用约束,等式约束对所有可行点都是起作用约束。
3. 拉格朗日乘子
基本的拉格朗日乘子法(又称为拉格朗日乘数法),就是求函数 f(x1,x2,...) 在 g(x1,x2,...)=0 的约束条件下的极值的方法。其主要思想是引入一个新的参数 λ (即拉格朗日乘子),将约束条件函数与原函数联系到一起,使能配成与变量数量相等的等式方程,从而求出得到原函数极值的各个变量的解
4.KKT条件
min.:f(x)
s.t.:gi(x)≤0,i=1,2,…,p,
hj(x)=0,k=1,2,…,q,
x∈Ω⊂Rn
KKT条件是指在满足一些有规则的条件下, 一个非线性规划(Nonlinear Programming)问题能有最优化解法的一个必要和充分条件. 这是一个广义化拉格朗日乘数的成果. 一般地, 一个最优化数学模型的列标准形式参考开头的式子, 所谓 Karush-Kuhn-Tucker 最优化条件,就是指上式的最优点x∗必须满足下面的条件:
- 1. 约束条件满足gi(x∗)≤0,i=1,2,…,p, 以及,hj(x∗)=0,j=1,2,…,q
- 2. ∇f(x∗)+∑i=1pμi∇gi(x∗)+∑j=1qλj∇hj(x∗)=0, 其中∇为梯度算子;
- 3. λj≠0且不等式约束条件满足μi≥0,μigi(x∗)=0,i=1,2,…,p
更多概念参考:https://blog.csdn.net/weixin_37352167/article/details/84675233
1.方向导数与梯度
方向导数是数值,表示某个方向上的导数
梯度为矢量,梯度方向上唯一存在最大的方向导数,梯度定义:
 2.二元函数的极值判断:
2.二元函数的极值判断:
设:二元函数 f(x,y)的稳定点为:(x0,y0),即:∂f(x0,y0)/∂x = ∂f(x0,y0)/∂y = 0;记::A=∂²f(x0,y0)/∂x²B=∂²f(x0,y0)/∂x∂yC=∂²f(x0,y0)/∂y²∆=AC-B²
如果:∆>0 A0,f(x0,y0) 为极小值;如果:∆0f(0,0)=0 为最小值。
求解函数极值方法:寻求函数整个定义域上的最大值和最小值是数学优化的目标。如果函数在闭合区间上是连续的,则通过极值定理存在整个定义域上的最大值和最小值。此外,整个定义域上最大值(或最小值)必须是域内部的局部最大值(或最小值),或必须位于域的边界上。
3.多元泰勒展开式:
凸优化的第一课,概念内容比较多。
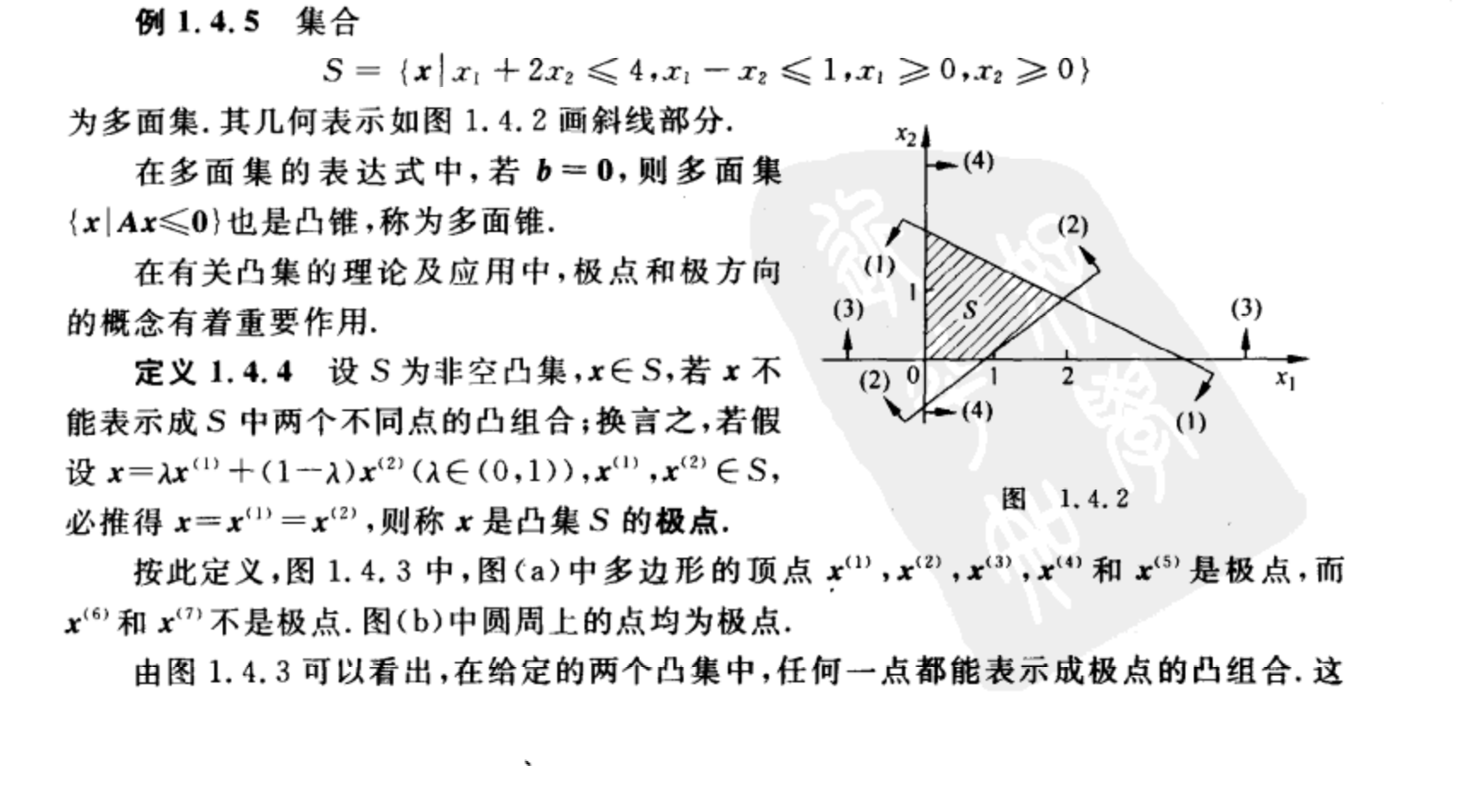
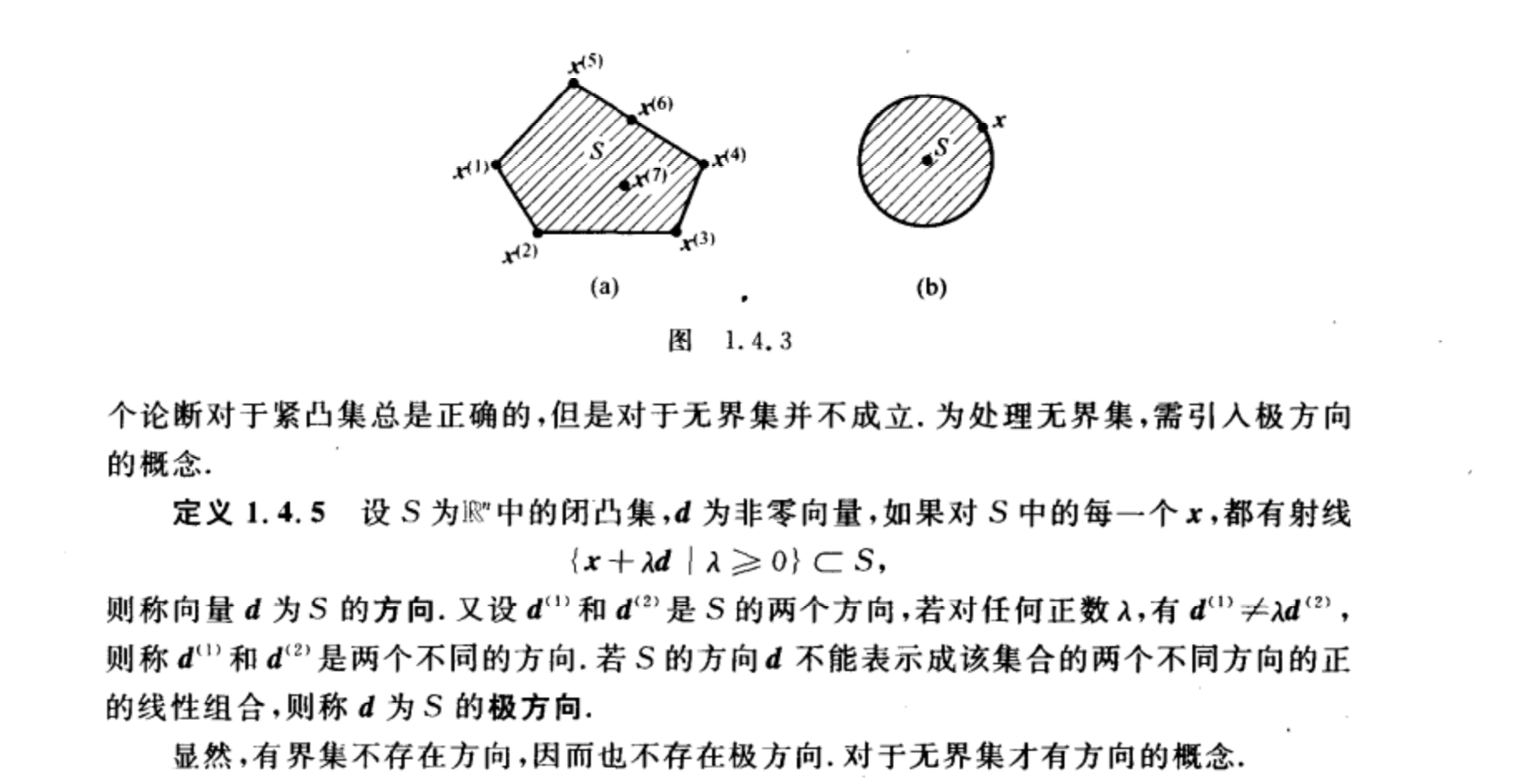
主要包括:凸集,超平面,半空间,锥,凸锥,射线,顶点,多面集,极点,极方向。参考老师给出的《最优化理论预算法》,具体概念和实例